We begin with the common state value function.
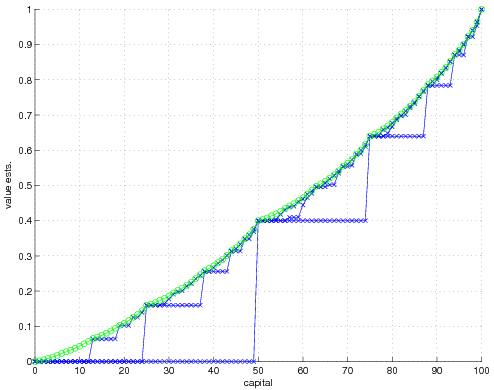
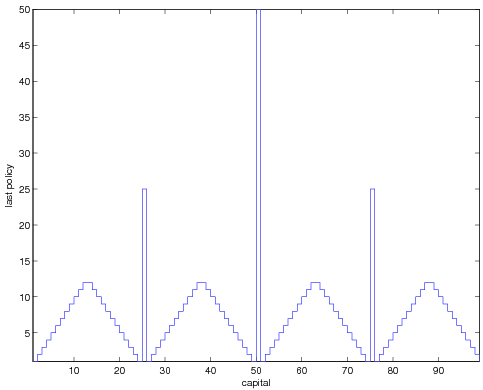
Now the optimal policy one obtains depends some very low level details. See the discussion here Here we will show a variety of the optimal policies we can obtain using the earlier code. If we follow the algorithm where we loop from the first action "1" to the last action and change our policy as we go only if the next policy is better than the previous by more than 10^(-8) we can obtain the result found in the book.
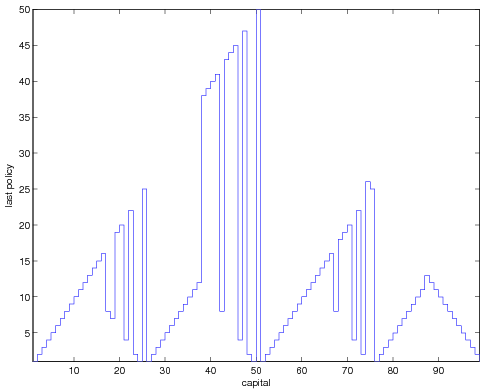
If we decrese this threshold so that we take any policy that is greater than the previous by any amount we obtain.
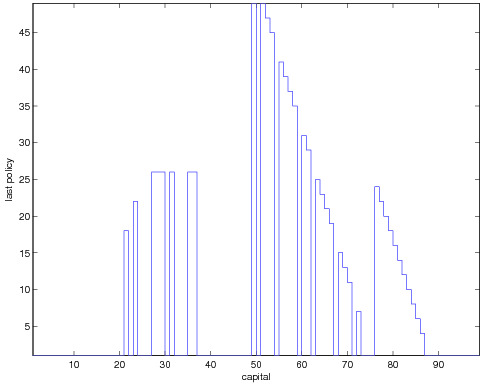
If we reverse the order of the actions when we consider them one at a time and still take the next policy even if it is only numerically greater than previous ones (i.e. eps_pol=0) we obtain
If we reverse the order of the policies but now only take policies that are greater by a threshold amount 10^(-8) we obtain a trivial policy
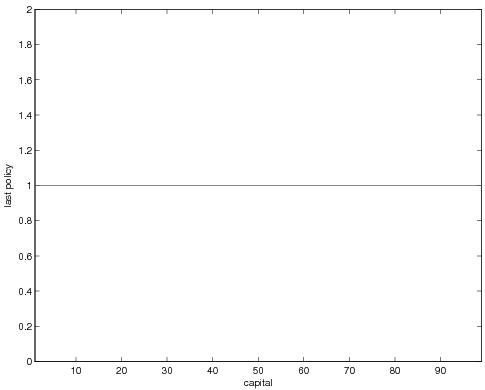
Various experiments can be performed in this way. If we take a different number of non-terminal states say an odd number say 1021 we find much more regular patterns. In that case we have
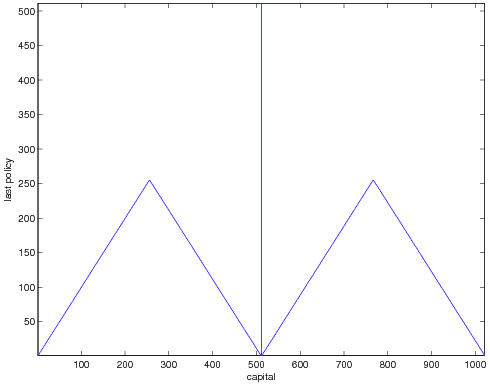
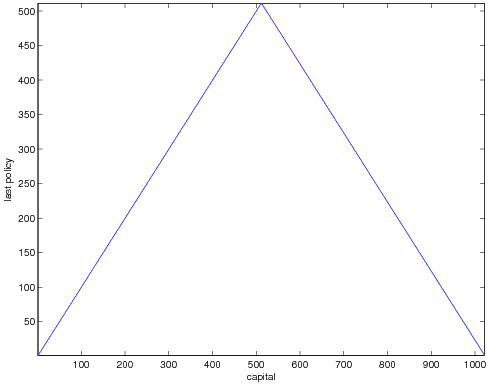
When the number of non-terminal states is 1022 we find our optimal policy given by.

---

John Weatherwax