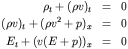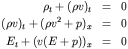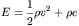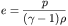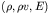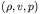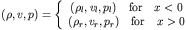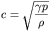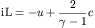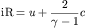A Riemann Solver For the Euler Equations of Gas Dynamics
by John Weatherwax
Introduction
Here you'll find code in FORTRAN
implementing a Riemann solver for the Euler equations of gas
dynamics. The Euler equations of gas dynamics are given by
the following system of three partial differential equations
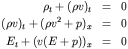 Where E is the total energy, i.e. the sum of the kinetic plus
the potential (internal) energy given by
Where E is the total energy, i.e. the sum of the kinetic plus
the potential (internal) energy given by
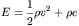 For a gamma gas law (ideal gas) it can be shown that the specific
internal energy e is given by
For a gamma gas law (ideal gas) it can be shown that the specific
internal energy e is given by
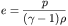 where gamma is a given constant (for air it is about 1.4). With
all of these definitions the system above is closed in terms
of the three conservative variables
where gamma is a given constant (for air it is about 1.4). With
all of these definitions the system above is closed in terms
of the three conservative variables
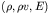 or the three primitive variables
or the three primitive variables
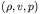 A Riemann problem is the solution to the above partial
differential equations with a discontinuous initial condition given
by
A Riemann problem is the solution to the above partial
differential equations with a discontinuous initial condition given
by
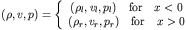 The Riemann solver itself is contained in the file "riemann_eu.f",
but a simple driver application is compiled when one builds the
package. The driver application is called "ne.out" and reads its
input from a text file called "newt.inp". In this text file one
specifies the left and right states, a Courant like number for use
in printing, and some flags that control output. Currently the code
is set to solve the "Sod" Riemann problem with initial conditions
given by
The Riemann solver itself is contained in the file "riemann_eu.f",
but a simple driver application is compiled when one builds the
package. The driver application is called "ne.out" and reads its
input from a text file called "newt.inp". In this text file one
specifies the left and right states, a Courant like number for use
in printing, and some flags that control output. Currently the code
is set to solve the "Sod" Riemann problem with initial conditions
given by
 The current flags settable in newt.inp are (they can be turned on
or off)
The current flags settable in newt.inp are (they can be turned on
or off)
- PRINT_NEWTON: Prints to the screen the initial
state and the pressure updates computed as the newton iterations
converge (at each timestep) as the intersection of the two wave
curves is found in the pressure velocity plane. Note: the
intersection of the wave curves is found by considering pressure
to be an independent variable and velocity the dependent
variable.
- PRINT_NEWTON_CONV: Prints the convergence steps of the
newton iterations into two files "pu_conv_l_test.dat", and
"pu_conv_r_test.dat" representing the newton iterates on each
of the two wave curves (left and right) in the pressure velocity
space respectively.
- PRINT_RP: Prints a summary of all the wave produced at for
the specific Riemann problem to be solved. This is saved in the
file "RP_test.dat". The information includes the states between
the three waves, the wave speeds, the wave types (shock,
rarefaction fan, or contact) and a flag variable denoting the
"significance" of the waves.
- PRINT_WC: Prints the left and right wave curves.
Specifically their projections onto the (pressure,velocity)
plane (in the files pu_curv_{l,r}_test.dat), the
(pressure,density) axis (in the files pr_curv_{l,r}_test.dat),
and the left and right Riemann invariants (in the file
iLiR_curv_{l,r}_test.dat). The ordering of the variables in the
files is given by the ordering in the filename. We define the
left and right Riemann invariants below.
- PRINT_INIT_WC: Currently not used.
Note an input to the routine riemann_eu.f requires the sound speed
of the state to each side of the interface. This is given by (and
can be computed with)
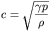 As an output from this Riemann solver we also produce the left and right
Riemann invariants for this system. The left going Riemann invariant is
constant on paths governed by the left facing characteristics (ones
traveling on dx/dt=u-c) and is also called a 3-Riemann invariant since it
is constant across 3-integral waves. For the Euler equations they are
defined by
As an output from this Riemann solver we also produce the left and right
Riemann invariants for this system. The left going Riemann invariant is
constant on paths governed by the left facing characteristics (ones
traveling on dx/dt=u-c) and is also called a 3-Riemann invariant since it
is constant across 3-integral waves. For the Euler equations they are
defined by
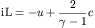 The right Riemann invariant is constant on paths governed by the right
going characteristics (dx/dt=u+c) and is also called a 1-Riemann invariant
since it is constant across 1-integral waves. For the Euler equations
they are defined by
The right Riemann invariant is constant on paths governed by the right
going characteristics (dx/dt=u+c) and is also called a 1-Riemann invariant
since it is constant across 1-integral waves. For the Euler equations
they are defined by
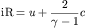 Note that these definitions of the Riemann invariants are twice that found
in the book:
Supersonic Flow and Shock Waves
Note that these definitions of the Riemann invariants are twice that found
in the book:
Supersonic Flow and Shock Waves
by R. Courant and K. O. Friedrichs
Interscience Publishers, Inc. New York, 1948
For further information one can also see the book:
Finite Volume Methods For Hyperbolic Problems
by Randall J. LeVeque
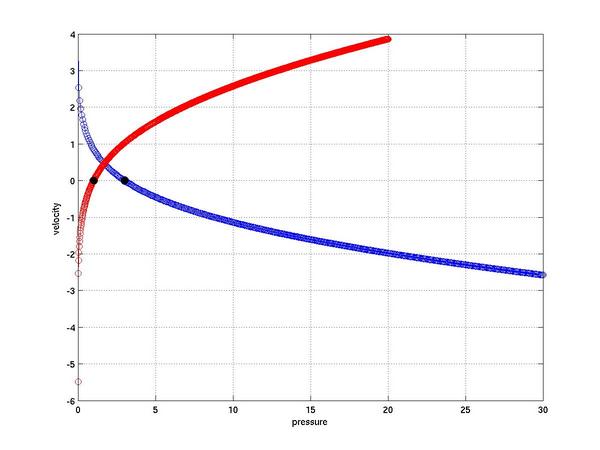
Solving the above Riemann problem produces the following left and
right wave curves (the wave curve through the left state is the
red curve and the wave curve through the right state is the blue curve)
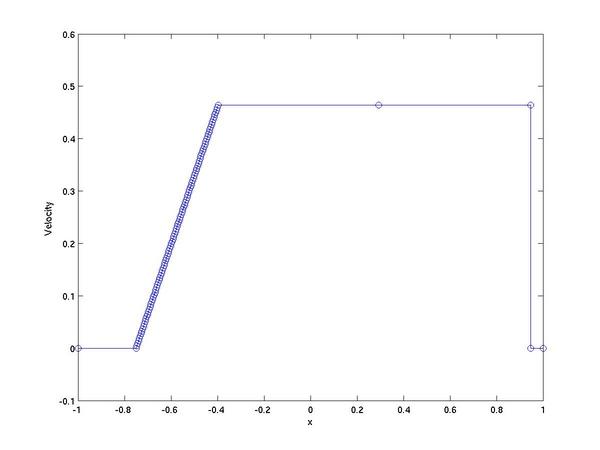
 With plots of the waves released in velocity at one unit of time
from the initial conditions (the central node tracks the location
of the contact) look like:
With plots of the waves released in velocity at one unit of time
from the initial conditions (the central node tracks the location
of the contact) look like:
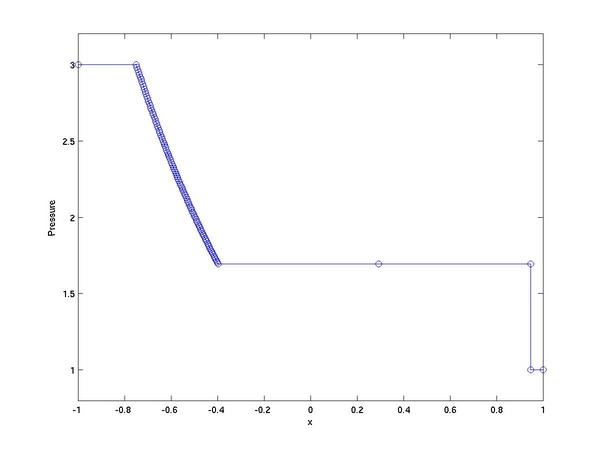
 The plot of pressure at one unit of time than the initial
conditions (the central node tracks the location of the contact)
look like:
The plot of pressure at one unit of time than the initial
conditions (the central node tracks the location of the contact)
look like:
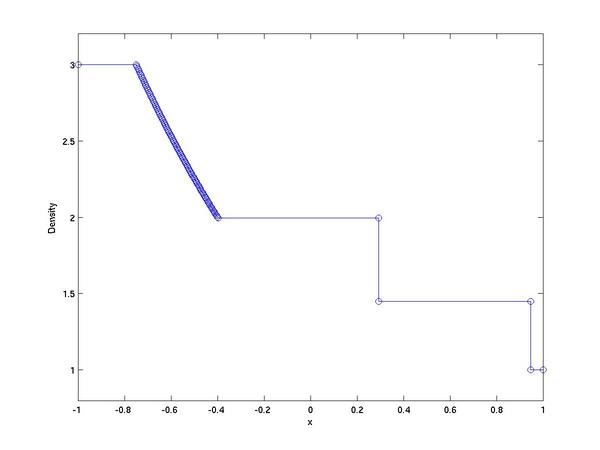
 The plots in density at one unit of time from the initial
conditions look like:
The plots in density at one unit of time from the initial
conditions look like:
 When the delivered code is built it contains an additional program
to compute the wave curves centered at a given state. The program
is called "twc.out"
Finally, here is the code
When the delivered code is built it contains an additional program
to compute the wave curves centered at a given state. The program
is called "twc.out"
Finally, here is the code
- Euler Riemann solver version 1.0
(.tar.gz)
(.zip)
- A simple Matlab function to extract information from the
wave curve files is given here
- A simple Matlab function to plot the output of the Riemann solver
is given here
As always, I am interested in hearing back if any errors are found to
exist.
John Weatherwax
Last modified: Sat Aug 19 10:20:07 EDT 2006