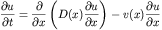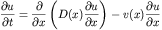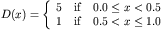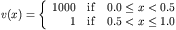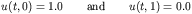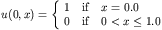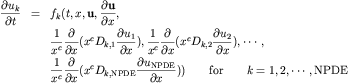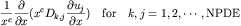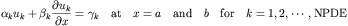PDEONE Example C:

Supposed one wanted to solve the following system of partial differential equations on the interval [0,1].

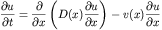With a discontinuous coefficient D(x) given by

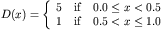and a spatially dependent discontinuous advection term v(x) given

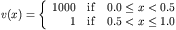We desire the solution of the PDE above with boundary conditions given by

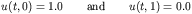With initial conditions given by

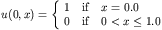This corresponds to the third example in the original reference to PDEONE (given above). This is quite simple to solve with the PDEONE gateway in octave. First the user must specify an octave function "F.m" which evaluates the right hand side of the PDE expressed in the following form

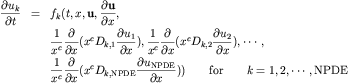
The incoming arguments to the octave function F.m are t,x,u,ux, and duxx. Here t is the scalar time, x the scalar grid point, u a vector of the NPDE unknowns, ux a vector of the x derivatives of these unknowns, and duxx is a matrix expressing the following derivatives

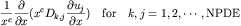
With the background we can write our F.m function for evaluating the right hand side of our PDEs. In addition to F.m, PDEONE requires the information on the diffusion coefficients D. This is provided in the form of a function D.m.

PDEONE requires the boundary conditions of the form

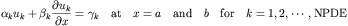To implement this in octave we must specify three boundary functions with input arguments t,x, and u (with the same meanings as above): BNDRY_ALPHA.m, BNDRY_BETA.m, and BNDRY_GAMMA.m.

Finally the user must specify the initial conditions. In this example this is given by the function elliptic_init.m. The two inputs to the initial condition function are t and x. Here t is a scalar input of time but in this case x is a vector of grid points where the initial conditions are desired. Note, that to work properly this function must be vectorized meaning that it can return a matrix (of dimension [NPDE,Number of Grid Points]) of initial conditions.

Once this code is written a person can call "pdeone.m". Here we present an example pdeone_Script.m driver file. Note: Since this problem is in Cartesian the constant c=0. Since this is the default, there is no need to specify anything additional. Finally, we can reap the benefits of our work by viewing the solution to our problem

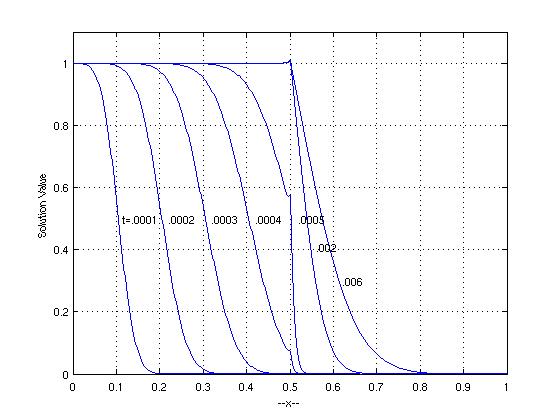
Note that this is a partial replica of a similar plot given in the Sincovec and Madsen paper. At this point the code begins to take an abnormally long time to move forward at each timestep. The reason for this behavior has to do with the solution becoming very stiff once the "wave" passes though the point x=0.5. From this point on the ODE solver rkc.f is not really a good choice and an implicit (unconditionally stable) method should be used instead. See the implementation of PDEONE with the GEARB integrator.

John Weatherwax

Last modified: Thu Jan 5 20:57:25 EST 2006