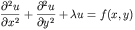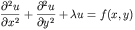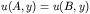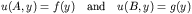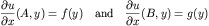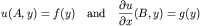Solving the 2D Cartesian Helmholtz Equation with Octave

This is some code I have written for solving the two-dimensional Helmholtz or Laplace's equation on a Cartesian grid. As such the code can solve:

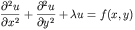
With a variety of admissable boundary conditions on the rectangular X and Y faces. Allowable boundary conditions for either the X coordinate direction of the Y coordinate direction consist of (shown for the x coordinate):

Periodic:
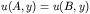
Dirichlet (on both faces):
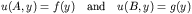
Neumann (on both faces):
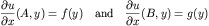
Mixed (on one face the solution is prescribed while on the other the derivative is prescribed):

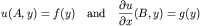
The numerical method implemented is the standard five point finite differences stencil. A potential drawback of this method is that it is only first order

This code is an octave gateway that calls the FORTRAN routine "hwscrt.f" originally part of the FISHPACK package of FORTRAN codes for the solution of elliptic partial differential equations.

Swarztrauber,P. and R. Sweet,
'Efficient FORTRAN Subprograms for the Solution of Elliptic Equations'
NCAR TN/IA-109, July, 1975, 138 pp.

An improvement provided by octave is that it allows easy parameter variations such as the number of grid points, wave number (for the Helmholtz Eq.) etc and does all memory allocation before calling the FORTRAN code.

Examples:

The example/driver program from the Swartztrauber and Sweet paper for HWSCRT (using octave) is given here. This is a elliptic PDE with a known exact solution.

If this software is used for any publications, I'd appreciate a reference. A sample bibtex entry is below


    @misc{weatherwaxHWSCRTG,

      author = "J L. Weatherwax",

      title  = "Software for solving PDE's with Octave",

      text   = "HWSCRTG: An Octave Gateway Routine to hwscrt.f",

      year   = "2005",

      url    = "http://web.mit.edu/wax/www/Software/hwscrt.html"
 
    }

I should mention that I am very interested in having people use this software and as such would be very willing to help get people started using it. As always, please send any comments to the address below.

The version 1.0 code is now finished.

John Weatherwax

Last modified: Fri Jul 14 04:00:51 EDT 2006