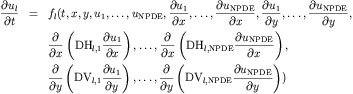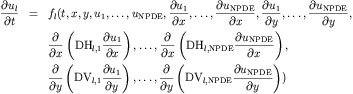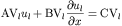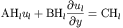Solving Partial Differential Equations with Octave

PDETWO

This is the first release of some code I have written for solving two-dimensional partial differential equations with Octave. The types of equations that can be solved with this method are of the following form (expressed for the l-th scalar component of u)


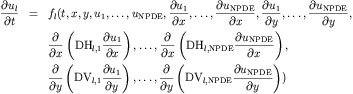
Here u is a vector (with NPDE components) of unknowns depending on both space (x,y) and time t. The spatial domain x and y is finite i.e. defined on [a1,b1] and [a2,b2] respectively. Boundary conditions depend on the partial differential equation (PDE) solved. The vertical boundary conditions are imposed in the octave code as equations of the following form


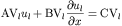
to be imposed at x=a1 and x=b1. While the horizontal boundary conditions are imposed in the octave code as equations of the following form


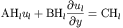
to be imposed at y=a2 and y=b2. The functional forms above are general enough that all types of boundary conditions Dirichlet, Neumann, or mixed can be handled. Edges without the application of boundary conditions are not allowed however so hyperbolic problems with this type of boundary conditions have to be modified to be solved with PDETWO. The initial conditions are supplied in the following form


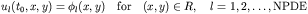
where R is the rectangular domain in which the problem is defined. The initial conditions are specified for each component of u at the initial time t_0. These initial conditions need not be consistent with the boundary conditions above. One potential drawback to the above formulation is that no provision is provided for solving equations containing cross derivative terms like


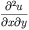
In the solution to equations of this form the user must specify octave functions (with a very similar format to Matlab functions) defining each of the functions described above for the specific problem at hand. As such it is very easy to modify and solve various different PDES. One can use the same functional call provided by the main PDETWO interface and solve vastly different PDE's by just change the octave functions. Various examples of this use are provided in the software below. The code is currently a C++/octave API wrapper that calls the core solution routine PDETWO described in the papers:

General Software for Two-Dimensional Nonlinear Partial Differential Equations
by David K. Melgaard, and Ricard F. Sincovec.
ACM Transactions on Mathematical Software (TOMS), Volume 7 Issue 1 (March 1981)
Pages: 106 - 125

and

Algorithm 565: PDETWO/PSETM/GEARB: Solution of Systems of Two-Dimensional Nonlinear Partial Differential
by David K. Melgaard, and Ricard F. Sincovec.
ACM Transactions on Mathematical Software (TOMS), Volume 7 Issue 1 (March 1981)
Pages: 126 - 135

The algorithm is based on the method of lines and uses finite difference to approximate the spatial derivatives. Second order finite difference approximations are performed automatically by the software and the user has a choice of ODE solvers to use in solving the resulting ordinary differential equations. In particular they can be solved with either of two main methods: an Adams' methods (with order between 1 and 12) and a stiff solver (of order between 1 and 5) of Gear. A few examples of using this code now follow.

Examples

The license in the ACM code only allows non-commercial usage of their codes. This license is too restrictive for the Free Software Foundation GNU copyleft and therefore the code cannot be included in the mainstream Octave sources. This license does however permit usage of this software for educational purposes.

Please reference this software in any publications that result from its use. A sample bibtex entry is below

@misc{weatherwaxPDETWOG,
author = "J L. Weatherwax",
title = "Software for solving PDE's with Octave",
text = "PDETWOG: An Octave Gateway Routine to pdetwo.f",
year = "2006",
url = "http://web.mit.edu/wax/www/Software/Code/PDETWO/Doc/pdetwo.html"
}

I should mention that I am very interested in having people use this software and as such would be very willing to help get people started using it. As always, please send any comments to the address below.

Code Versions:

Installation

General Notes:

The code was compiled on a 686 athalon chip and thus should not need to be recompiled if you are using a similar chipset. If this is not the case, to rebuild the function you will need a FORTRAN 77 compiler and a C++ compiler in addition to the mkoctfile script to produce the dynamically linked function pdetwog.oct.

More information about dynamically linked functions for octave can be found in the: "Dal Segno al Coda" found here.

Linux/Unix:

To run all the examples provided you first must extract the source into a local directory. In this example, lets assume that you downloaded a file named "PDETWO.x.y". Where x and y are the major and minor version numbers PDETWO distribution. First unzip and untar the distribution using

gunzip PDETWO.x.y.tar.gz
tar -xvf filename.tar

Where filename is the name of the version of code downloaded. Next, change into the newly created directory

cd PDETWO.x.y

In that directory, one should see subdirectories containing the various octave files used to specify the different PDE's. The first numerical PDE example from the paper above is in the subdirectory is named "EG1". To run the code corresponding to this PDE definition. We must first insure that octave can find these files and not any others with the same name. As such there should be a file called .octaverc in this top most directory. Open this file in an editor and change the line to read (if it is not already)

LOADPATH = ['Code_Examples//EG1//', LOADPATH];

Now start octave in this top most directory, with an invocation like octave &

The LOADPATH command will set the path so that when octave is started in the given directory it will find the required pdetwo_Script.m in the EG1 directory and no other. This setting will then set the octave path to include the needed files for the first example discribed above. Then at the octave prompt type

pdetwo_Script

and the given PDE will be solved numerically for you with a few plots produced.

Windows:

I developed the PDETWO package on a Linux system and have never tested it on Windows, but it should work with if the proper compilers are provided and you remake the dynamically liked function pdetwog.oct. See the discussion above. If you are able to get this to work I would be happy to hear about it including tricks you had to know or perform to get everything to work.

To Do:

John Weatherwax
Last modified: Wed Jul 12 21:07:33 EDT 2006